Przykładowe rozwiązania

0,75x – długość krótszej przekątnej rombu

Pole rombu można opisać wyrażeniem ½·x·0,75x, zatem

½·x·0,75x = 96

0,375x² = 96
x² = 256
x = 16
0,75x = 12

Przekątne rombu (12 cm, 16 cm) są prostopadłe i dzielą się na połowy. Długość boku rombu oblicz z twierdzenia Pitagorasa:

6² + 8² = a²
36 + 64 = a²
a² = 100
a = 10

Obwód rombu jest równy 4a = 4 · 10 cm = 40 cm

Odpowiedź: Obwód rombu jest równy 40 cm.

y – długość krótszej przekątnej rombu

⁴⁄₃ y – długość dłuższej przekątnej rombu

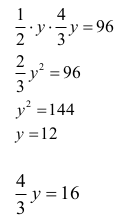
Przekątne rombu (12 cm, 16 cm) są prostopadłe i dzielą się na połowy, stąd oblicz długość boku rombu:

6² + 8² = a²
36 + 64 = a²
a² = 100
a = 10

Obwód rombu jest równy 4a = 4 · 10 cm = 40 cm

Odpowiedź: Obwód rombu jest równy 40 cm.