Odpowiedź:
Przykładowe rozwiązania
Sposób 1.

Prostokąt, z którego wycięto narożniki w kształcie kwadratu, ma boki długości
(3 + 2a) i (1 + 2a).
Pole tego prostokąta opisuje wyrażenie: (3 + 2a) · (1 + 2a)
Po wycięciu narożników pole prostokąta zmniejszyło się o pola czterech kwadratów – każdy o polu a2.
Po wycięciu narożników pole prostokąta zmniejszyło się o pola czterech kwadratów – każdy o polu a2.
Pole zacieniowanej figury opisuje zatem wyrażenie:
(3 + 2a) · (1 + 2a) – 4a2 = 3 + 6a + 2a + 4a2 – 4a2 = 8a + 3
Wartość otrzymanego wyrażenia dla a = 2,5 jest równa:
8 · 2,5 + 3 = 20 + 3 = 23
Sposób 2.
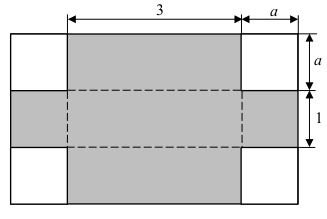
Zacieniowaną figurę można podzielić w różny sposób na kilka figur, np. tak, jak pokazano na rysunku.
Mamy dwa prostokąty o bokach długości 3 i a, jeden prostokąt o bokach długości 3 i 1 oraz dwa prostokąty o bokach długości a i 1.
Pole zacieniowanej figury opisuje zatem wyrażenie:
2 · 3a + 3 · 1 + 2 · a = 6a + 3 + 2a = 8a + 3
Wartość otrzymanego wyrażenia dla a = 2,5 jest równa:
8 · 2,5 + 3 = 20 + 3 = 23