Odpowiedź:
Przykładowe pełne rozwiązania
Pierwszy sposób
Dzielimy prostokąt na dwa prostokąty. Dwa boki otrzymanych prostokątów oznaczamy tak, jak pokazano na rysunku.
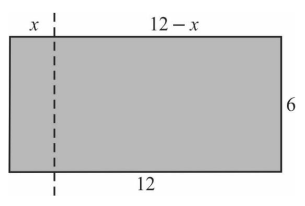
Obwód mniejszego prostokąta jest równy 2 · x + 2 · 6 = 2x + 12
Obwód większego prostokąta jest równy 2 (12 – x) + 2 · 6 = 36 – 2x
Obwód jednego prostokąta jest 2 razy większy od obwodu drugiego, co zapisujemy za pomocą równania.
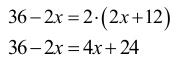
12 = 6 x
x = 2
x = 2
Odpowiedź: Prostokąt o mniejszym obwodzie ma wymiary 6 i 2.
Drugi sposób
Dzielimy prostokąt na 2 kwadraty o obwodach 24.
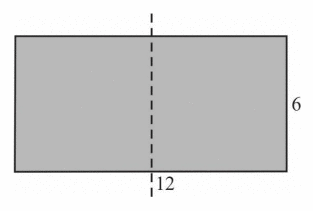
Suma obwodów kwadratów jest równa 48. Zauważmy, że jeśli przesuniemy linię podziału, suma obwodów otrzymanych figur się nie zmieni.
Łączny obwód szukanych prostokątów jest równy 48, stosunek tych obwodów jest równy 2 : 1.Zatem obwód mniejszego prostokąta jest równy 48 : 3 = 16
Skoro jeden bok tego prostokąta jest równy 6, to drugi bok ma długość 16⁄2 – 6 = 2.
Odpowiedź: Prostokąt o mniejszym obwodzie ma wymiary 6 i 2.
Trzeci sposób
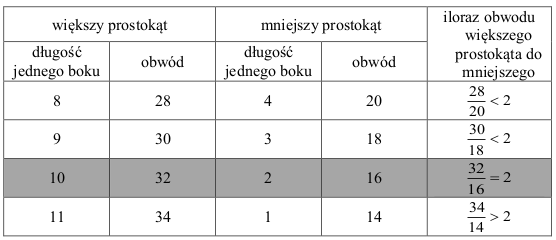
Dzielimy prostokąt na 2 kwadraty o obwodach 24.
Przesuwamy linię podziału i otrzymujemy dwa prostokąty. W każdym z nich długość jednego boku zmienia się, a drugiego wynosi 6. Sprawdzamy, jaki jest iloraz obwodów otrzymanych prostokątów.
Przesuwamy linię podziału i otrzymujemy dwa prostokąty. W każdym z nich długość jednego boku zmienia się, a drugiego wynosi 6. Sprawdzamy, jaki jest iloraz obwodów otrzymanych prostokątów.
Odpowiedź: Prostokąt o mniejszym obwodzie ma wymiary 6 i 2.