Odpowiedź:
Przykładowe pełne rozwiązania
Pierwszy sposób
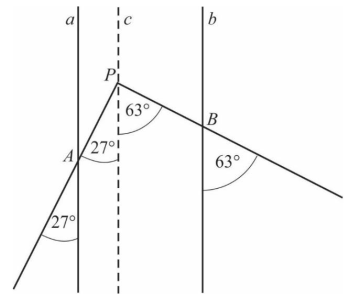
Przez punkt P prowadzimy prostą c równoległą do a i b. Dzieli ona kąt APB na dwie części,
z których jedna jest kątem odpowiadającym do 27°, a druga – do 63°, zatem
|∢APB| = 27° + 63° = 90°.
Kąt APB jest kątem prostym.
Drugi sposób
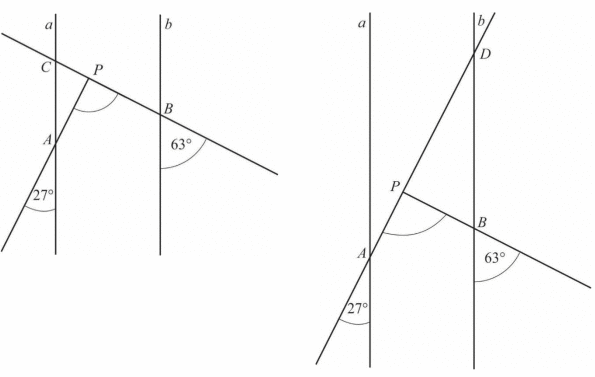
Przedłużamy półprostą PB do przecięcia z prostą a w punkcie C lub półprostą PA do przecięcia
z prostą b w punkcie D. Ustalamy miary dwóch kątów w powstałych trójkątach APC lub BPD.
Jeden z kątów jest kątem wierzchołkowym, a drugi – kątem odpowiadającym do kątów
odpowiednio 63° i 27°.
Obliczamy miarę trzeciego kąta w powstałych trójkątach APC lub BPD.
|∢APC| = 180° – (27° + 63°) = 90°
Kąt APB jest kątem przyległym do kąta APC, czyli jest kątem prostym.
|∢BPD| = 180° – (27° + 63°) = 90°
Kąt APB jest kątem przyległym do kąta BPD, czyli jest kątem prostym.
Kąt APB jest kątem przyległym do kąta APC, czyli jest kątem prostym.
|∢BPD| = 180° – (27° + 63°) = 90°
Kąt APB jest kątem przyległym do kąta BPD, czyli jest kątem prostym.
Trzeci sposób
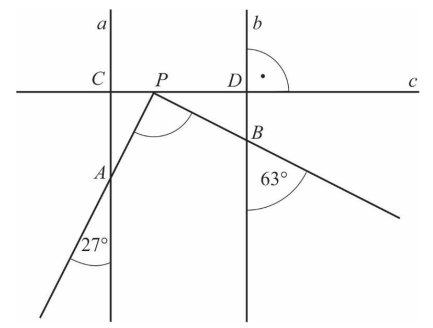
Przez punkt P prowadzimy prostą c prostopadłą do a i b. Wyznacza ona dwa trójkąty prostokątne APC i BPD. Ustalamy miary kątów ostrych tych trójkątów.
|∢CPA| = 90° – 27° = 63° oraz |∢BPD| = 90° – 63° = 27°
|∢APB| = 180° – (27° + 63°) = 90°
Kąt APB jest kątem prostym.
Kąt APB jest kątem prostym.
Czwarty sposób
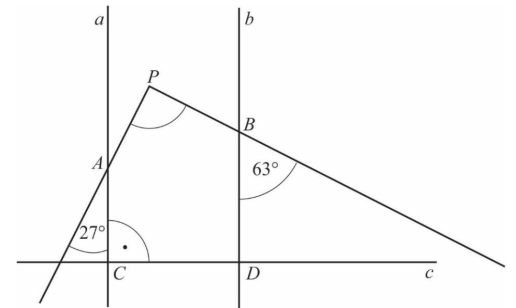
Prowadzimy prostą c prostopadłą do a i b tak, aby powstał pięciokąt wypukły. Ustalamy miary kątów rozwartych tego pięciokąta.
|∢CAP| = 180° – 27° = 153° oraz |∢PBD| = 180° – 63° = 117°
|∢APB| = 540° – (90° + 90° + 117° + 153°) = 90°
Kąt APB jest kątem prostym.
|∢APB| = 540° – (90° + 90° + 117° + 153°) = 90°
Kąt APB jest kątem prostym.
Piąty sposób
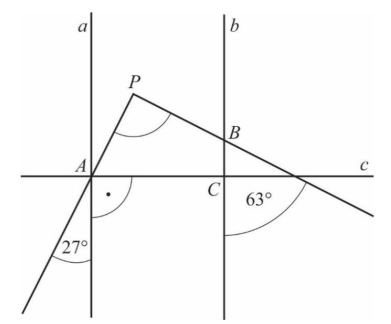
Przez punkt A prowadzimy prostą c prostopadłą do a i b. Wyznacza ona czworokąt ACBP.
Ustalamy miary dwóch kątów czworokąta.
Ustalamy miary dwóch kątów czworokąta.
|∢CBP| = 180° – 63° = 117° oraz |∢CAP| = 90° – 27° = 63°
|∢APB| = 360° – (90° + 117° + 63°) = 90°
Kąt APB jest kątem prostym.
|∢APB| = 360° – (90° + 117° + 63°) = 90°
Kąt APB jest kątem prostym.