Odpowiedź:
Przykładowe pełne rozwiązania
Pierwszy sposób
Jeśli długość boku małego kwadratu oznaczymy przez x, to duży kwadrat ma bok długości 3x, a średni ma bok długości 1,5x.
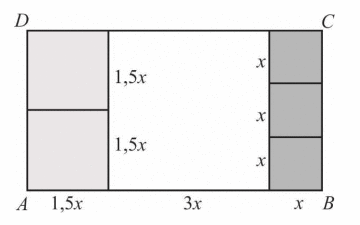
Pole prostokąta ABCD: 3 · x2 + (3x) + 2 · (1,5x2) = 16,5 x2
Pole dużego kwadratu: (3x)2 = 9x2
Połowa pola prostokąta ABCD to 8,25x2
Zatem duży kwadrat zajmuje ponad połowę pola prostokąta ABCD.
Drugi sposób
Jeśli długość boku małego kwadratu oznaczymy przez x, to duży kwadrat ma bok długości 3x, a średni ma bok długości 1,5x.
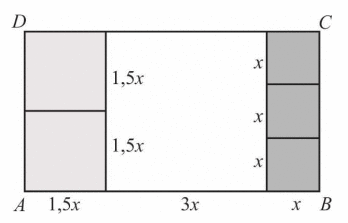
Obliczmy długość odcinka AB, na którym postawiono prostokąt ABCD: 1,5x + 3x + x = 5,5x.
Podzielmy prostokąt ABCD na trzy prostokąty o tej samej wysokości AD: pierwszy złożony z 2 średnich kwadratów, drugi – duży kwadrat, a trzeci złożony z 3 małych kwadratów.
Duży kwadrat ma bok długości 3x.
Połowa długości odcinka AB to 2,75x.
2,75 x · 3x < 3x · 3x
Zatem duży kwadrat zajmuje ponad połowę pola prostokąta ABCD.
Połowa długości odcinka AB to 2,75x.
2,75 x · 3x < 3x · 3x
Zatem duży kwadrat zajmuje ponad połowę pola prostokąta ABCD.
Trzeci sposób
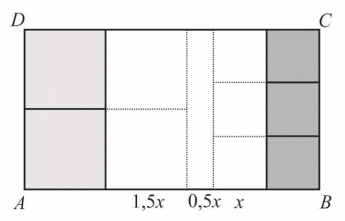
Zauważmy, że dwa średnie kwadraty zajmują połowę powierzchni dużego kwadratu, a trzy
małe kwadraty zajmują powierzchnię mniejszą niż połowa powierzchni dużego kwadratu.
Zatem duży kwadrat zajmuje ponad połowę pola prostokąta ABCD.
Czwarty sposób
Bok średniego kwadratu jest o połowę mniejszy od boku dużego kwadratu. Stąd pole średniego kwadratu stanowi ¼ pola dużego kwadratu.
PŚr = ¼ PD
Bok małego kwadratu stanowi 1⁄3 boku dużego kwadratu. Stąd pole małego kwadratu stanowi 1⁄9 pola dużego kwadratu.
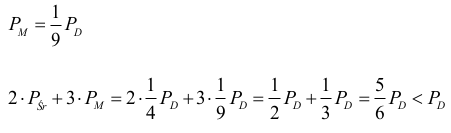
Zatem duży kwadrat zajmuje ponad połowę pola prostokąta ABCD.