x – początkowa ilość wody w drugim zbiorniku (w litrach)

4x – początkowa ilość wody w pierwszym zbiorniku (w litrach)

4x + 6 = 2(x + 6)
4x + 6 = 2x + 12
x = 3
W pierwszym zbiorniku było na początku 4 · 3 = 12 litrów wody, a w drugim były 3 litry.
12 + 6 = 18
3 + 6 = 9

Po dolaniu:
– w pierwszym zbiorniku jest 18 litrów wody
– w drugim zbiorniku jest 9 litrów wody.
18 + 9 = 27

Odpowiedź: Razem w obu zbiornikach jest 27 litrów wody.

x - początkowa ilość wody w pierwszym zbiorniku (w litrach)

¹⁄₄ –początkowa ilość wody w drugim zbiorniku (w litrach)

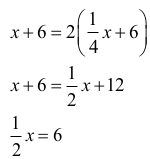
x = 12

W pierwszym zbiorniku było na początku 12 litrów wody, a w drugim były ¹⁄₄ · 12 = 3 litry.

12 + 6 = 18
3 + 6 = 9
Po dolaniu:
– w pierwszym zbiorniku jest 18 litrów wody
– w drugim zbiorniku jest 9 litrów wody.
18 + 9 = 27

Odpowiedź: Razem w obu zbiornikach jest 27 litrów wody.