Odpowiedź:
Przykładowe pełne rozwiązania
Pierwszy sposób
Zauważmy, że kwadrat ABCD można podzielić na 6 trójkątów przystających do trójkąta AED.
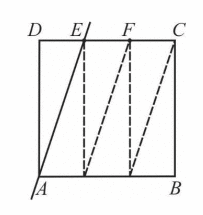
P = 6 · 24 = 144 (cm2)
Odpowiedź: Pole kwadratu ABCD jest równe 144 cm2.
Drugi sposób
Zauważmy, że trójkąt AED ma pole 3 razy mniejsze od pola połowy kwadratu. Jest zatem 6 razy mniejsze od pola kwadratu ABCD.
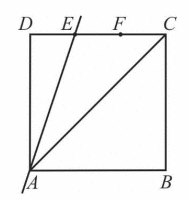
P = 6 · 24 = 144 (cm2)
Odpowiedź: Pole kwadratu ABCD jest równe 144 cm2.
Trzeci sposób
Oznaczmy długość boku DE trójkąta jako a. Wtedy bok DA trójkąta ma długość 3a.
Z wzoru na pole trójkąta otrzymujemy równanie:
Z wzoru na pole trójkąta otrzymujemy równanie:
24 = ½ · a · 3a
3a2 = 48
a = 4
3a = 3 · 4 = 12
P = 6 · 24 = 144 (cm2)
a = 4
3a = 3 · 4 = 12
P = 6 · 24 = 144 (cm2)
Odpowiedź: Pole kwadratu ABCD jest równe 144 cm2.